FP in C++: Function composition

Walletfox.com

support@walletfox.com

2018

Learn about function composition

• Preconditions
• Composition of unary functions
• Commutativity
• Multi-argument composition
• Associativity
• Composition vs application

Function composition is one of the central concepts of functional programming

Combining functions enables creating complex functionality

Output becomes input

Output of the inner function becomes the input of the outer function.

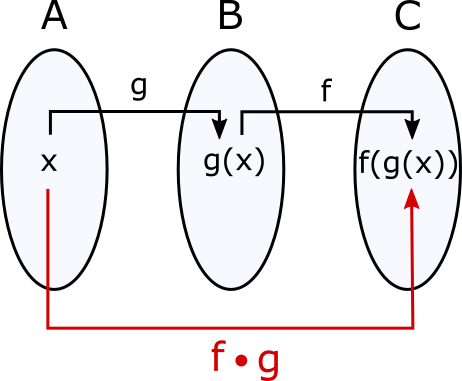
Type match is essential

Composition requires output-to-input type match.

Not all functions can be composed

Function f expects a single value, however g returns an array.

This problem can be solved with monads and Kleisli composition.

Q: What is the result of the composition f(g(x))?

Use nested lambda to express composition

auto compose = [](auto f, auto g) {
  return [=](auto x) {
    return f(g(x));
  };
};

auto op = compose(f2, f1);

Unary function composition only.

Let's look at a concrete example

Assume, you have temperature expressed in ℉. Does this value fall within the room temperature range 20 - 25 ℃ ?

We have the following functions at hand

double fahrenheitToCelsius(double fahr){
    return (fahr - 32) * 5.0 / 9.0;
}

bool isRoomTemperature(double t){
    return (t >= 20.0 && t < 25.0) ? true : false;
}

All we need to do is compose functions

Notice the order, we compose from right to left.

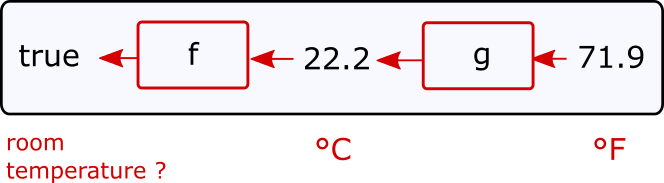
auto op = compose(isRoomTemperature, fahrenheitToCelsius);
auto val1 = op(71.9); // returns 1, i.e. room temperature
auto val2 = op(50.3); // returns 0, i.e. not room temperature

We could have created a distinct function for this purpose

auto opComposed(double fahr){
    return isRoomTemperature(fahreheitToCelsius(fahr));
}

int main() {
   auto val = opComposed(71.9); // room temperature
}

However, composition gives us elegance and generality

auto vecBool = map(vecTemp, 
               compose(isRoomTemperature, fahrenheitToCelsius));

The composed function can be directly fed into higher-order functions, such as map and filter.

An operation is commutative if changing the order of the operands does not change the result.

Q: Compose f(g(x)), then g(f(x))

Did you get tricked by the previous question?

Composition is not commutative in general

The result happened to be the same, because the functions were mutual inverses.

Let's create a variation of the temperature example. We are interested in calculating BMI of a person and determining whether he is overweight.

We have the following functions at hand

double bmi(double weight, double height){
    return weight / height / height;
}

bool isOverweight(double bmi){
    return (bmi >= 25.0) ? true : false;
}

We need to supply 2 values to calculate BMI

Multi-argument composition requires parameter pack

auto compose = [](auto f, auto g) { 
    return [=](auto&& ... x) { 
        return f(g(x...)); 
    }; 
};

Passing multiple parameters becomes simple

auto op = compose(isOverweight, bmi);
auto val1 = op(59.8, 1.7); // returns 0, i.e. false
auto val2 = op(73.0, 1.52); // returns 1, i.e. true

Certain binary operations (e.g. +) exhibit associative property. Rearranging parentheses won't change the value of an expression.

Composition is always associative

(f • g) • h = f • (g • h) compose(compose(f,g),h)=compose(f,compose(g,h))