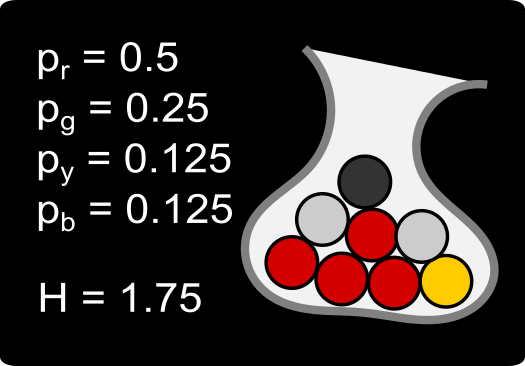Introduction

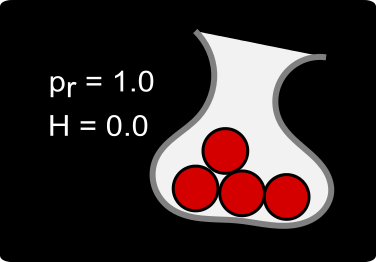
In simple terms, Shannon entropy expresses the level of disorganization using probabilities. Look at the examples below. The first pouch has the lowest entropy, i.e. level of disorganisation, because the balls it contains have the same color. Anytime you decide to pull a ball from the pouch, you would get a ball of red color with certainty.

The second pouch has higher entropy than the first one because you can no longer be certain about the color of the ball. Nevertheless, you are more likely to draw a ball of red color.

The third pouch has the highest entropy because we have the least information regarding the likelihood of drawing a red ball.

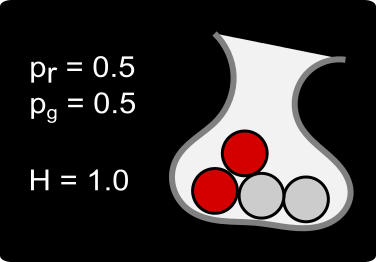
The general formula for Shannon's entropy can be seen below.

Given the probabilities of events (in our case, drawing a ball of red color, drawing a ball of grey color) we can compute the entropy by multiplying the individual probabilities with their logarithms and summing them up.

---

Implementation details - map / fold

The general idea of the computation is to accomplish the multiplication for each probability with the help of map and sum up the partial results with the help of fold. This can be seen below.

The first step of the entropy computation is the transformation of probabilities into multiplicates of probabilities and their respective logarithms. This can be accomplished with the help of the higher-order function map.

auto map = [](auto op, auto col)
{
   std::transform(std::begin(col), std::end(col), 
                  std::begin(col), op);
   return col;
};

This restricted version of map can be used provided the input and output type of the collection is the same. The input collection is passed by value, i.e. std::transform works on the copy of the input collection. The input collection won't be modified.

The second step of the computation, i.e. the summation of the partial results, can be accomplished with the help of the higher-order function fold.

auto foldl = [](auto op, auto init, auto col) {
    return std::accumulate(std::begin(col), 
                 std::end(col), init, op);
};

Implementation details - papply / compose

In addition to the above mentioned higher-order functions we are also going to use compose for function composition and papply for function application. This is because we would like to express the final entropy function without concrete arguments, i.e. using the so called point-free style.

auto papply = [](auto f, auto... args) {
    return [=](auto... rargs) {
        return f(args..., rargs...);
    };
};

auto compose = [](auto f1, auto f2) {
  return [=](auto x) {
    return f1(f2(x));
  };
};

The complete solution can be seen below. We introduce partial application to create a function capable of calculating multiplicates of probabilities and their logarithms on yet an unknown collections (opMap). Similarly, we use partial application to create a function that will sum up elements of yet an unknown collection (opSum). Finally, we compose the two partially applied functions into the final function opEntropy. We test our composed function an example with 8 balls of 4 different colors. 4 balls are red, 2 balls grey, 1 yellow and 1 black.

int main()
{
    auto opMap = papply(map, [](auto p){
                             return -p*std::log2(p);});
    auto opSum = papply(foldl, std::plus<>(),0.0);
    auto opEntropy = compose(opSum, opMap);

    std::vector<double> v = {0.5,0.25,0.125,0.125};
    std::cout << opEntropy(v) << '\n'; // outputs 1.75

    return 0;
}